כשרובנו רואים מכונה מושכת טאפי מתרחקת על מטיילת תיירותית, אנו חושבים על סוכר מתוק ומתוק. ז'אן-לוק טייפולט חושב על מתמטיקה מתוקה ומתוקה. כמתמטיקאי יישומי מאוניברסיטת ויסקונסין-מדיסון, טיפיו מתעניין במיוחד באופן שבו חומרים כמו טאפי מתערבבים: במכונה, הממתק נמתח ומקופל שוב ושוב כדי לשלב אוויר ולפתח את המרקם הקל והלעוס שלו. כאשר הוא מושך, המלבן המקורי של הטאפי נמתח יותר ויותר - אורכו גדל באופן אקספוננציאלי ביחס זהה בכל פעם. יחס מתיחה זה מה שמעניין את טיפייולט.
תוכן קשור
- שוקולד להמיס הוכחה, גומי מודפס תלת מימד ופטנטים ממתקים אחרים מרתקים
כשאדם מושך טאפי, הם בדרך כלל ייקחו את גוש הממתקים ויתחבו אותו מעל וו, ויביאו את שני הקצוות. ואז הם ייקחו את הקטע המקופל הזה ויתחברו אותו שוב מעל הוו, שיכפילו את האורך וכן הלאה. במילים אחרות, "הדרך האנושית לעשות זאת היא גורם הכפל של 2", אומר טיפיפו. מושכים מכניים יכולים להצליח יותר, ולעתים קרובות מניבים מספרים גדולים ואקזוטיים לא רציונליים כגורמי המתיחה שלהם.
מתברר כי משיכת טאפי ניתנת לעיצוב לפי שדה מופשט של מתמטיקה המכונה דינמיקה טופולוגית, בעיקרו חקר שינויים ארוכי טווח בקנה מידה גדול לאורך זמן במרחב מתמטי. (אם המילה טופולוגית נשמעת מוכרת, זה היה בחדשות לאחרונה כחלק מפרס נובל לפיזיקה השנה.) לאותה מתמטיקה המתארת משיכת טאפי יש גם יישומים רציניים יותר: תהליכים תעשייתיים רבים, כולל ניפוח זכוכית והכנת תרופות, דורשים נוזלים צמיגיים שיש לערבב בדרכים שדומות יותר למשיכת טאפי מאשר ערבוב שמנת לקפה. "אם אתה מנסה לעורר דברים צמיגים באמת, כמו משחות בתעשיית התרופות, אתה לא יכול פשוט לטלטל אותם, " אומר טיפיפ. "זה לא כמו לערבב צבע."
טייפולט הבין משיכת טאפי כדוגמא לערבוב צמיגי במשך זמן רב, אך רק לאחרונה הוא באמת בדק את ההיסטוריה של מושכי הטאפי כדי לחשוף את הסודות המתמטיים שלהם. התוצאה של טיול זה לפטנטים היסטוריים היא המאמר האחרון שלו "היסטוריה מתמטית של מושכי טאפי" שפורסם בשרת ההדפסה המקדימה arXiv ביולי.
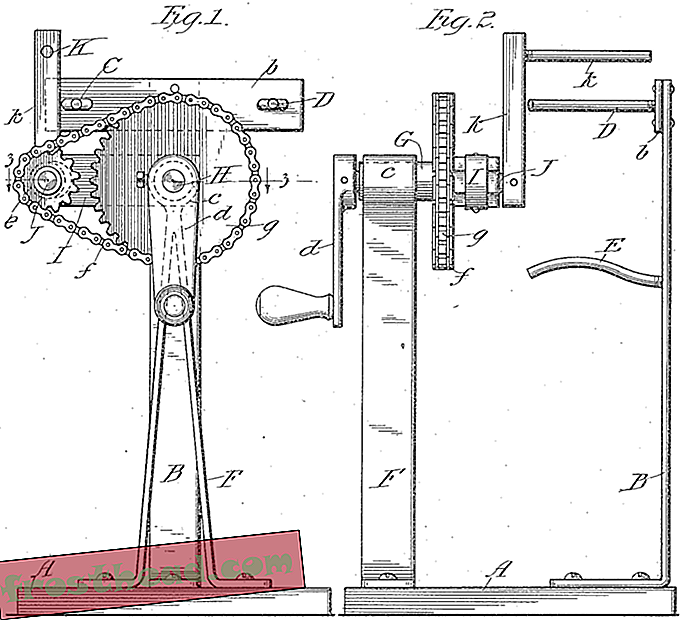תמונה מפטנט מכונות טופי משנת 1916 המופיעה במחקר של טיפיפ. באופן ספציפי, האזור שהוביל לצלילה העמוקה של טאפי שלו הוא חקר מה שמכונה מיפוי פסאודו-אנושוב. פסאודו-אנושוב הוא דרך מפוארת לתאר תהליך בו צורה דו-ממדית נמתחת באופן אקספוננציאלי לכיוון אחד בזמן שהיא מתכווצת בכיוון השני. מבחינה מתמטית המחקר של מיפוי פסאודו-אנושוב הוא חדש יחסית. "בשנות ה -70 וה -80 אנשים ניסו מאוד למצוא דוגמאות", אומר טיפיו. למרבה האירוניה הם היו שם לאורך כל הדרך בפטנטים למושכי טאפי. "מכיוון שמתמטיקאים מעולם לא הביטו בספרות זו, הם מעולם לא היו יודעים שהם קיימים, " הוא אומר.
בעודו מסרק באמצעות פטנטים של מושך טפי, טיפף טיול בקרב בקרב משפטי שהלך עד לבית המשפט העליון. הנושא שנדון בפרשת 1921, הילדרת נ 'מסטוראס, היה באופן הרחב שיש לפרש פטנט משנת 1900 על מושך טפי. כלומר: האם דגם מאוחר יותר שנעשה על ידי מישהו אחר היה רק שיפור קל, או שמא מדובר במכשיר אחר? חלק מכריע בטיעון היה עד כמה שונה הפטנט משנת 1900 מקודמו בשנת 1893 (שככל הנראה לא יוצר מעולם). חוות דעתו של בית המשפט, שנכתב על ידי השופט הראשי וויליאם הווארד טאפט, "מראה תפיסה נוקבת של הדינמיקה הטופולוגית", כותב טיפיפו במאמרו.
בית המשפט הכיר בכך שהמכשיר הקודם - שהיה לו שני ווים בלבד - לא יכול היה למתוח את הטופי במידה האקספוננציאלית הנדרשת ליצירת קונדיטוריות יעילה. בחוות דעתו של טאפט נאמר:
עם שני ווים בלבד לא יכול היה להיות הקפות של הממתק, מכיוון שלא היה סיכה שלישית שתעסוק את הממתק מחדש בזמן שהיא הוחזקה בין שני הסיכות האחרות. תנועתם של שני הסיכות במעגלים קונצנטריים אולי תמתח אותה מעט ומעוררת אותה, אך היא לא תמשוך אותה במובן האמנות.
Thiffeault כותב, "חוות הדעת של בית המשפט העליון מציגה את התובנה הבסיסית שלפחות שלוש מוטות נדרשות כדי לייצר צמיחה מהירה כלשהי."
Thiffeault אומר שיש כיום שני מושכי טפי סטנדרטיים, האחד עם שלושה מוטות ואחד עם ארבעה. יש להם במקרה אותו גורם מתיחה. זה קשור ליחס המכונה יחס כסף, 1+ √2, או בערך 2.414, בן דוד מעט פחות זוהר ביחס הזהב המפורסם יותר.
העובדה ששני מושכי הטאפי הסטנדרטיים נמתחים ביחס הכסף מעניינת מכיוון שיחס הכסף הוא - במובן המתמטי המדויק - אופטימלי. עם זאת, טיפוח מזהיר כי לא כל כך קל לדרג מושכי טפי שונים, אפילו כשאתה מכיר את גורמי המתיחה שלהם: "יש לזה היבט תפוחים ותפוזים שקשה מאוד לעקוף אותו", הוא אומר. למושך אחד יש יותר מוטות וייקח זמן רב יותר לחזור למצב הראשוני שלו מאשר אחר, או שהוא עשוי לדרוש מומנט רב יותר או הילוכים מורכבים יותר. אז למרות שהמתמטיקה אכן נותנת תובנה מסוימת עד כמה מושכים מושכי טאפי, היא לא מספרת את הסיפור השלם.
מחקריו של טיפיפו במושכי טאפי העניקו לו השראה ותלמידו לתואר הראשון אלכס פלנגן לבנות מודל משלהם. הם רצו לבדוק אם הם יכולים להגדיל את היעילות מבלי לשנות את ההילוכים במידה רבה, ובסופו של דבר הכינו מושך חדש עם 6 מוטות המבוסס על תיבת ההילוכים של חולץ 4 המוט הסטנדרטי. "הסיבה לכך שהצלחנו לעשות זאת היא שעכשיו יש לנו מתמטיקה", אומר טיפיפ. הם יכלו לדגם את המכונה בהרחבה במחשב ולעקוף חלק ניכר מהניסוי והטעייה עם מכשירים פיזיים אמיתיים שהיו צריכים להמציא קודם לכן. מכשיר 6 המוטים, שהוא עדיין רק אב-טיפוס, מותח טפי בערך פי שניים מהמושכים הסטנדרטיים בכל מחזור.
עד כה, יצרני מושך טאפי לא בדיוק הכו את דלתו של טיפיפו כדי לקבל עצות לגבי אופטימיזציה של העיצובים שלהם - ביג טאפי מסתפק ככל הנראה בסטטוס קוו המתוח שלה - אך יש לו תקוות כי לשיטותיו עשויות להיות השפעות בענפים אחרים. מלבד ניפוח זכוכית, מקום הגיוני אחד לאופטימיזציה של ערבוב הוא תעשיית התרופות. אחרי הכל, ערבוב ויטמינים ותרופות דורש בקרת איכות גבוהה במיוחד: היצרנים "מוכנים לשלם הרבה כסף על ערבוב מושלם" מכיוון שהם "לא יכולים לסבול מולטי ויטמין רע אחד מתוך 1000", אומר טיפיפולט. אז יום אחד, רוקחים אולי נותנים קריאה מתוקה למושכי הטאפי המסורים של השנה.
ואז שוב, זה עשוי להיות מעט מתיחה.
